|
|
| (未显示2个用户的15个中间版本) |
| 第1行: |
第1行: |
|
|
{{tex}} |
|
|
|
|
{{Book |
|
{{Book |
|
| author = {{w|伟烈亚力}}口译<br>{{w|李善兰}}笔述<br>{{w|伊莱亚斯·罗密士}}原著 |
|
| author = {{w|伟烈亚力}}口译<br>{{w|李善兰}}笔述<br>{{w|伊莱亚斯·罗密士}}原著 |
| 第9行: |
第11行: |
|
|
|
|
|
'''《代微积{{ruby|拾|shè}}级》''',由英国汉学家、来华传教士{{w|伟烈亚力}}(Alexander Wylie,1815年4月6日-1887年2月10日)口译,清代数学家{{w|李善兰}}(1811年1月22日-1882年12月9日)笔述;1859年由上海{{w|墨海书馆}}(The London Missionary Society Press)出版。原著为美国数学家{{w|伊莱亚斯·罗密士}}(Elias Loomis,1811年8月7日-1889年8月15日)于1851年出版的'''《解析几何和微积分初步》(''Elements of Analytical Geometry and of The Differential and Integral Calculus'')'''。 |
|
'''《代微积{{ruby|拾|shè}}级》''',由英国汉学家、来华传教士{{w|伟烈亚力}}(Alexander Wylie,1815年4月6日-1887年2月10日)口译,清代数学家{{w|李善兰}}(1811年1月22日-1882年12月9日)笔述;1859年由上海{{w|墨海书馆}}(The London Missionary Society Press)出版。原著为美国数学家{{w|伊莱亚斯·罗密士}}(Elias Loomis,1811年8月7日-1889年8月15日)于1851年出版的'''《解析几何和微积分初步》(''Elements of Analytical Geometry and of The Differential and Integral Calculus'')'''。 |
|
|
|
|
|
据考证,李善兰翻译所用的底本,应为1852年再版的版本,而非1851年的初版(内容差别较大)。原著在1874年改版,在此之前有不下20个版次(包括1856年的第6版、1859年的第10版、1864年的第17版、1868年的第19版等),畅销程度可见一斑。 |
|
|
|
|
|
1872年(明治5年),这本书被福田半译至日文,但书中并未使用李善兰创立的对应符号系统(参见[[#符号]]),而是使用原著的符号。 |
|
|
|
|
|
需要注意的是,这本书中的定义以今天的眼光来看并不严谨。一方面,当时的微积分学基础并不牢固,(ε, δ)-极限定义还未出现,书中仍然只使用未严格定义的无穷小量来定义概念;另一方面,这本书本身就是入门教材,不应过于晦涩难懂。 |
|
需要注意的是,这本书中的定义以今天的眼光来看并不严谨。一方面,当时的微积分学基础并不牢固,(ε, δ)-极限定义还未出现,书中仍然只使用未严格定义的无穷小量来定义概念;另一方面,这本书本身就是入门教材,不应过于晦涩难懂。 |
|
|
|
|
|
<gallery> |
|
<gallery> |
|
Analytical Geometry.jpg|代(解析几何) |
|
Elements of Analytical Geometry and of The Differential and Integral Calculus (Chinese, 1859, 1).pdf|page=1|代(解析几何) |
|
Differential.jpg|微(微分) |
|
Elements of Analytical Geometry and of The Differential and Integral Calculus (Chinese, 1859, 2).pdf|page=1|微(微分) |
|
Integral.jpg|积(积分) |
|
Elements of Analytical Geometry and of The Differential and Integral Calculus (Chinese, 1859, 3).pdf|page=1|积(积分) |
|
</gallery> |
|
</gallery> |
|
|
|
|
| 第27行: |
第33行: |
|
* [[:File:Elements of Analytical Geometry and of The Differential and Integral Calculus (Chinese, 1859, 3).pdf|卷十七-卷十八(积分)]]([[Media:Elements of Analytical Geometry and of The Differential and Integral Calculus (Chinese, 1859, 3).pdf|源文件]]) |
|
* [[:File:Elements of Analytical Geometry and of The Differential and Integral Calculus (Chinese, 1859, 3).pdf|卷十七-卷十八(积分)]]([[Media:Elements of Analytical Geometry and of The Differential and Integral Calculus (Chinese, 1859, 3).pdf|源文件]]) |
|
* [[:File:Elements of Analytical Geometry and of The Differential and Integral Calculus.pdf|英文原著]]([[Media:Elements of Analytical Geometry and of The Differential and Integral Calculus.pdf|源文件]]) |
|
* [[:File:Elements of Analytical Geometry and of The Differential and Integral Calculus.pdf|英文原著]]([[Media:Elements of Analytical Geometry and of The Differential and Integral Calculus.pdf|源文件]]) |
|
|
|
|
|
== 原文 == |
|
|
* [[/卷一|卷一]]([[/卷一/英文|英文]]) |
|
|
|
|
|
== 符号 == |
|
== 符号 == |
| 第32行: |
第41行: |
|
=== 字母 === |
|
=== 字母 === |
|
|
|
|
|
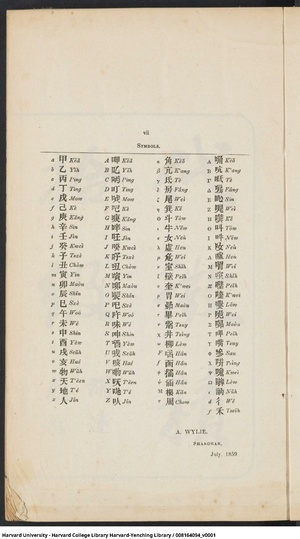
[[File:Symbol Table.jpg|right|thumb|符号表,注意希腊字母{{lang|el|Ρ}}与{{lang|el|Μ}}对应颠倒]] |
|
[[File:Elements of Analytical Geometry and of The Differential and Integral Calculus (Chinese, 1859, 1).pdf|page=11|right|thumb|符号表,注意希腊字母{{lang|el|Ρ}}与{{lang|el|Μ}}对应颠倒]] |
|
|
|
|
|
在书中,小写{{w|拉丁字母}}以天干(10个)、地支(12个)和物(w)、天(x)、地(y)、人(z)对应;小写{{w|希腊字母}}以{{w|二十八宿}}的前24个对应。大写字母将小写字母对应的汉字左侧加上“口”来表示,即使加上口字旁的字已存在,也按照小写的读音来读(例如小写的v对应“亥”,那么大写的V对应的“咳”也读作hài)。另外还有一些专用的符号单独对应。 |
|
在书中,小写{{w|拉丁字母}}以天干(10个)、地支(12个)和物(w)、天(x)、地(y)、人(z)对应;小写{{w|希腊字母}}以{{w|二十八宿}}的前24个对应。大写字母将小写字母对应的汉字左侧加上“口”来表示,即使加上口字旁的字已存在,也按照小写的读音来读(例如小写的v对应“亥”,那么大写的V对应的“咳”也读作hài)。另外还有一些专用的符号单独对应。 |
| 第143行: |
第152行: |
|
| 癸 |
|
| 癸 |
|
! {{lang|el|Κ}} |
|
! {{lang|el|Κ}} |
|
| {{ruby|𠯆|nǔ}} |
|
| {{ruby|𠯆|nǚ}} |
|
! {{lang|el|κ}} |
|
! {{lang|el|κ}} |
|
| 女 |
|
| 女 |
| 第1,393行: |
第1,402行: |
|
在卷十的开头,可以看到那句经典名句: |
|
在卷十的开头,可以看到那句经典名句: |
|
|
|
|
|
{{from|微分之數有二,一曰常數,一曰變數;變數以天地人物等字代之,常數以甲乙子丑等字代之。<br><br>凡式中常數之同數俱不變。如直線之式爲<math>地\xlongequal{\qquad}甲天\bot乙</math>,則線之甲與乙,俱僅有一同數任在何點永不變,而天與地之同數則每點皆變也。<br><br>'''凡此變數中函彼變數,則此爲彼之函數。'''<br><br>如直線之式爲<math>地\xlongequal{\qquad}甲天\bot乙</math>,則地爲天之函數;又平圜之式爲<math>地\xlongequal{\qquad}\sqrt{味^二\top甲^二}</math>,味爲半徑,天爲正弦,地爲餘弦;橢圓之式爲<math>地\xlongequal{\qquad}</math>{{sfrac|呷|{{RareChar|𠮙|⿰口乙}}}}<math>\sqrt{二呷天\top天^二}</math>,皆地爲天之函數也。<br><br>設不明顯天之函數,但指地爲天之因變數,則如下式<math>天\xlongequal{\qquad}函(地) \ 地\xlongequal{\qquad}函(天)</math>,此天爲地之函數,亦地爲天之函數。|《代微積拾級·卷十 微分一·例》}} |
|
{{from|微分之數有二,一曰常數,一曰變數;變數以天地人物等字代之,常數以甲乙子丑等字代之。<br><br>凡式中常數之同數俱不變。如直線之式爲<math>地\xlongequal{\quad}甲天\bot乙</math>,則線之甲與乙,俱僅有一同數任在何點永不變,而天與地之同數則每點皆變也。<br><br>'''凡此變數中函彼變數,則此爲彼之函數。'''<br><br>如直線之式爲<math>地\xlongequal{\quad}甲天\bot乙</math>,則地爲天之函數;又平圜之式爲<math>地\xlongequal{\quad}\sqrt{味^二\top甲^二}</math>,味爲半徑,天爲正弦,地爲餘弦;橢圓之式爲<math>地\xlongequal{\quad}</math>{{sfrac|呷|{{RareChar|𠮙|⿰口乙}}}}<math>\sqrt{二呷天\top天^二}</math>,皆地爲天之函數也。<br><br>設不明顯天之函數,但指地爲天之因變數,則如下式:<math>天\xlongequal{\quad}函(地)</math>,<math>地\xlongequal{\quad}函(天)</math>,此天爲地之函數,亦地爲天之函數。|《代微積拾級·卷十 微分一·例》}} |
|
|
|
|
|
<center>[[File:Elements of Analytical Geometry and of The Differential and Integral Calculus (Chinese, 1859, 2).pdf|page=4|300px]][[File:Elements of Analytical Geometry and of The Differential and Integral Calculus (Chinese, 1859, 2).pdf|page=3|300px]]</center> |
|
<div style="text-align: center;">[[File:Elements of Analytical Geometry and of The Differential and Integral Calculus (Chinese, 1859, 2).pdf|page=4|300px]][[File:Elements of Analytical Geometry and of The Differential and Integral Calculus (Chinese, 1859, 2).pdf|page=3|300px]]</div> |
|
|-| |
|
|-| |
|
English= |
|
English= |
|
原文如下: |
|
原文如下: |
|
{{from|A<span style{{=}}"font-size: 70%;>RTICLE</span> (157.) I<span style{{=}}"font-size: 70%;>N</span> the Differential Calculus, as in Analytical Geometry, there are two classes of quantities to be considered, viz., ''variables'' and ''constants''.<br><br>Variable quantities are generally represented by the last letters of the alphabet, ''x'', ''y'', ''z'', etc., and any values may be assigned to them which will satisfy the equations into which they enter.<br><br>Constant quantities are generally represented by the firstletters of the alphabet, ''a'', ''b'', ''c'', etc., and these always retain the same values throughout the same investigation.<br><br>Thus, in the equation of a straight line, <br><center><math>y=ax+b</math>,</center>the quantities a and b have but one value for the same line, while ''x'' and ''y'' vary in value for every point of the line.<br><br>(158.) '''One variable is said to be a ''function'' of another variable, when the first is equal to a certain algebraic expression containing the second.''' Thus, in the equation of a straight line <br><center><math>y=ax+b</math>,</center>''y'' is a function of ''x''. <br><br>So, also, in the equation of a circle, <br><center><math>y=\sqrt{R^2-x^2}</math>;</center>and in the equation of the ellipse, <br><center><math>y=\frac{B}{A}\sqrt{2Ax-x^2}</math>.</center>(159.) When we wish merely to denote that ''y'' is ''dependent'' upon ''x'' for its value, without giving the particular expression which shows the value of ''x'', we employ the notation<br><center><math>y=F(x)</math>, or <math>y=f(x)</math>,<br><span style{{=}}"text-align: left; float: left;">or</span><math>x=F(y)</math>, or <math>x=f(y)</math>,</center>which expressions are read, ''y'' is a function of ''x'', or ''x'' is a function of ''y''. |
|
{{from|1=A<span style{{=}}"font-size: 0.6rem;>RTICLE</span> (157.) I<span style{{=}}"font-size: 0.6rem;>N</span> the Differential Calculus, as in Analytical Geometry, there are two classes of quantities to be considered, viz., ''variables'' and ''constants''.<br><br>Variable quantities are generally represented by the last letters of the alphabet, ''x'', ''y'', ''z'', etc., and any values may be assigned to them which will satisfy the equations into which they enter.<br><br>Constant quantities are generally represented by the firstletters of the alphabet, ''a'', ''b'', ''c'', etc., and these always retain the same values throughout the same investigation.<br><br>Thus, in the equation of a straight line, <br><div style="text-align: center;"><math>y=ax+b</math>,</div>the quantities a and b have but one value for the same line, while ''x'' and ''y'' vary in value for every point of the line.<br><br>(158.) '''One variable is said to be a ''function'' of another variable, when the first is equal to a certain algebraic expression containing the second.''' Thus, in the equation of a straight line <br><div style="text-align: center;"><math>y=ax+b</math>,</div>''y'' is a function of ''x''. <br><br>So, also, in the equation of a circle, <br><div style="text-align: center;"><math>y=\sqrt{R^2-x^2}</math>;</div>and in the equation of the ellipse, <br><div style="text-align: center;"><math>y=\frac{B}{A}\sqrt{2Ax-x^2}</math>.</div>(159.) When we wish merely to denote that ''y'' is ''dependent'' upon ''x'' for its value, without giving the particular expression which shows the value of ''x'', we employ the notation<br><div style="text-align: center;"><math>y=F(x)</math>, or <math>y=f(x)</math>,<br><span style{{=}}"text-align: left; float: left;">or</span><math>x=F(y)</math>, or <math>x=f(y)</math>,</div>which expressions are read, ''y'' is a function of ''x'', or ''x'' is a function of ''y''.|2=''Elements of Analytical Geometry and of The Differential and Integral Calculus'', Differential Calculus, Section I, Definitions and First Principles}} |
|
|''Elements of Analytical Geometry and of The Differential and Integral Calculus'', Differential Calculus, Section I}} |
|
|
|
|
|
|
<center>[[File:Elements of Analytical Geometry and of The Differential and Integral Calculus.pdf|page=124|300px]][[File:Elements of Analytical Geometry and of The Differential and Integral Calculus.pdf|page=125|300px]]</center> |
|
<div style="text-align: center;">[[File:Elements of Analytical Geometry and of The Differential and Integral Calculus.pdf|page=124|300px]][[File:Elements of Analytical Geometry and of The Differential and Integral Calculus.pdf|page=125|300px]]</div> |
|
</tabber> |
|
</tabber> |
|
|
|
|
| 第1,413行: |
第1,421行: |
|
同样是卷十,可以看到微分的定义: |
|
同样是卷十,可以看到微分的定义: |
|
|
|
|
|
{{from|'''函數與變數之變比例俱謂之微分''',用彳號記之。如 <math>戌\xlongequal{\qquad}天^三</math>,則得比例 {{RareChar|𢓍|⿰彳天}} : [[File:Differential u.svg|16px]] <math>:: 一 : 三天^二</math>。{{RareChar|𢓍|⿰彳天}}[[File:Differential u.svg|16px]],爲天與戌之微分。后皆仿此,用表天與戌之變比例。以一四兩率相乘,二三兩率相乘,則得[[File:Differential u.svg|16px]]<math>\xlongequal{\qquad}三天^二</math>{{RareChar|𢓍|⿰彳天}}。此顯函數戌之變比例,等于 三天<sup>二</sup> 乘變數天之變比例。以{{RareChar|𢓍|⿰彳天}}約之,得{{sfrac|{{RareChar|𢓍|⿰彳天}}|[[File:Differential u.svg|16px]]}}<math>\xlongequal{\qquad}三天^二</math>。此顯變數之變比例,約函數之變比例,等于函數之微係數也。如戌爲天之函數,三天 爲戌之微係數,此舉立方以㮣其餘。|《代微積拾級·卷十 微分一·論函數微分》}} |
|
{{from|'''函數與變數之變比例俱謂之微分''',用彳號記之。如 <math>戌\xlongequal{\quad}天^三</math>,則得比例 {{RareChar|𢓍|⿰彳天}} : [[File:Differential u.svg|16px]] <math>:: 一 : 三天^二</math>。{{RareChar|𢓍|⿰彳天}}[[File:Differential u.svg|16px]],爲天與戌之微分。后皆仿此,用表天與戌之變比例。以一四兩率相乘,二三兩率相乘,則得[[File:Differential u.svg|16px]]<math>\xlongequal{\quad}三天^二</math>{{RareChar|𢓍|⿰彳天}}。此顯函數戌之變比例,等于 三天<sup>二</sup> 乘變數天之變比例。以{{RareChar|𢓍|⿰彳天}}約之,得{{sfrac|{{RareChar|𢓍|⿰彳天}}|[[File:Differential u.svg|16px]]}}<math>\xlongequal{\quad}三天^二</math>。此顯變數之變比例,約函數之變比例,等于函數之微係數也。如戌爲天之函數,三天 爲戌之微係數,此舉立方以㮣其餘。|《代微積拾級·卷十 微分一·論函數微分·第二款》}} |
|
<center>[[File:Elements of Analytical Geometry and of The Differential and Integral Calculus (Chinese, 1859, 2).pdf|page=19|300px]][[File:Elements of Analytical Geometry and of The Differential and Integral Calculus (Chinese, 1859, 2).pdf|page=18|300px]]</center> |
|
<div style="text-align: center;">[[File:Elements of Analytical Geometry and of The Differential and Integral Calculus (Chinese, 1859, 2).pdf|page=19|300px]][[File:Elements of Analytical Geometry and of The Differential and Integral Calculus (Chinese, 1859, 2).pdf|page=18|300px]]</div> |
|
|-| |
|
|-| |
|
English= |
|
English= |
|
原文如下: |
|
原文如下: |
|
{{from|(170.) '''The rate of variation of a function or of any variable quantity is called its ''differential''''', and is denoted by the letter ''d'' placed before it. Thus, if<br><center><math>u=x^3</math>,</center>then<br><center><math>dx:du::1:3x^2</math>.</center>The expressions ''dx'', ''du'' are read differential of ''x'', differential of ''u'', and denote the rates of variation of ''x'' and ''u''.<br><br>If we multiply together the extremes and the means of the preceding proportion, we have<br><center><math>du=3x^2dx</math>,</center>which signifies that the rate of increase of the function ''u'' is 3''x''<sup>2</sup> times that of the variable ''x''.<br><br>If we divide each member of the last equation by ''dx'', we have<br><center><math>\frac{du}{dx}=3x^2</math>,</center>which expresses the ratio of the rate of variation of the function to that of the independent variable, and is called the ''differential coefficient'' of ''u'' regarded as a function of ''x''.|''Elements of Analytical Geometry and of The Differential and Integral Calculus'', Differential Calculus, Proposition II}} |
|
{{from|1=(170.) '''The rate of variation of a function or of any variable quantity is called its ''differential''''', and is denoted by the letter ''d'' placed before it. Thus, if<br><div style="text-align: center;"><math>u=x^3</math>,</div>then<br><div style="text-align: center;"><math>dx:du::1:3x^2</math>.</div>The expressions ''dx'', ''du'' are read differential of ''x'', differential of ''u'', and denote the rates of variation of ''x'' and ''u''.<br><br>If we multiply together the extremes and the means of the preceding proportion, we have<br><div style="text-align: center;"><math>du=3x^2dx</math>,</div>which signifies that the rate of increase of the function ''u'' is 3''x''<sup>2</sup> times that of the variable ''x''.<br><br>If we divide each member of the last equation by ''dx'', we have<br><div style="text-align: center;"><math>\frac{du}{dx}=3x^2</math>,</div>which expresses the ratio of the rate of variation of the function to that of the independent variable, and is called the ''differential coefficient'' of ''u'' regarded as a function of ''x''.|2=''Elements of Analytical Geometry and of The Differential and Integral Calculus'', Differential Calculus, Section I, Differentiation of Algebraic Functions, Proposition II - Theorem}} |
|
|
|
|
|
<center>[[File:Elements of Analytical Geometry and of The Differential and Integral Calculus.pdf|page=131|300px]]</center> |
|
<div style="text-align: center;">[[File:Elements of Analytical Geometry and of The Differential and Integral Calculus.pdf|page=131|300px]]</div> |
|
|
|
|
|
注意,时至今日,微分号为了与量区别而记作<math>\mathrm{d}</math>,书中的微分号仍然是斜体<math>d</math>。 |
|
注意,时至今日,微分号为了与量区别而记作<math>\mathrm{d}</math>,书中的微分号仍然是斜体<math>d</math>。 |
|
|
|
|
</tabber> |
|
</tabber> |
|
|
|
|
|
书中所称“Differential Coefficient”,译作“微系数”,今天称作'''导数(Derivative)'''。无论是中英文,这种古老的说法都已很罕见。 |
|
|
|
|
|
== 积分 == |
|
== 积分 == |
| 第1,431行: |
第1,442行: |
|
在卷十七,定义了积分: |
|
在卷十七,定义了积分: |
|
|
|
|
|
{{from|積分爲微分之還原,其法之要,在識別微分所由生之函數。如已得 天<sup>二</sup> 之微分爲 二天{{RareChar|𢓍|⿰彳天}},則有 二天{{RareChar|𢓍|⿰彳天}},即知所由生之函數爲 天<sup>二</sup>,而 天<sup>二</sup> 即爲積分。<br><br>'''已得微分所由生之函數爲積分。'''而積分或有常數附之,或無常數附之,既不能定,故式中恒附以常數,命爲{{RareChar|𠰳|⿰口丙}}。{{RareChar|𠰳|⿰口丙}}或有同數,或爲〇,須攷題乃知。<br><br>來本之視微分,若函數諸小較之一,諸小較并之,即成函數。故微分之左係一禾字,指欲取諸微分之積分也。如下式 禾二天{{RareChar|𢓍|⿰彳天}}<math>\xlongequal{\qquad} 天^二 \bot</math>{{RareChar|𠰳|⿰口丙}}。來氏說今西國天算家大率不用,而惟用此禾字,取其一覽了然也。|《代微積拾級·卷十七 積分一·總論》}} |
|
{{from|積分爲微分之還原,其法之要,在識別微分所由生之函數。如已得 天<sup>二</sup> 之微分爲 二天{{RareChar|𢓍|⿰彳天}},則有 二天{{RareChar|𢓍|⿰彳天}},即知所由生之函數爲 天<sup>二</sup>,而 天<sup>二</sup> 即爲積分。<br><br>'''已得微分所由生之函數爲積分。'''而積分或有常數附之,或無常數附之,既不能定,故式中恒附以常數,命爲{{RareChar|𠰳|⿰口丙}}。{{RareChar|𠰳|⿰口丙}}或有同數,或爲〇,須攷題乃知。<br><br>來本之視微分,若函數諸小較之一,諸小較并之,即成函數。故微分之左係一禾字,指欲取諸微分之積分也。如下式 禾二天{{RareChar|𢓍|⿰彳天}}<math>\xlongequal{\quad} 天^二 \bot</math>{{RareChar|𠰳|⿰口丙}}。來氏說今西國天算家大率不用,而惟用此禾字,取其一覽了然也。|《代微積拾級·卷十七 積分一·總論》}} |
|
<center>[[File:Elements of Analytical Geometry and of The Differential and Integral Calculus (Chinese, 1859, 3).pdf|page=4|300px]][[File:Elements of Analytical Geometry and of The Differential and Integral Calculus (Chinese, 1859, 3).pdf|page=3|300px]]</center> |
|
<div style="text-align: center;">[[File:Elements of Analytical Geometry and of The Differential and Integral Calculus (Chinese, 1859, 3).pdf|page=4|300px]][[File:Elements of Analytical Geometry and of The Differential and Integral Calculus (Chinese, 1859, 3).pdf|page=3|300px]]</div> |
|
|-| |
|
|-| |
|
English= |
|
English= |
|
原文如下: |
|
原文如下: |
|
{{from|A<span style{{=}}"font-size: 70%;>RTICLE</span> (291.) T<span style{{=}}"font-size: 70%;>HE</span> Integral Calculus is the reverse of the Differential Calculus, its object being to determine the expression or function from which a given differential has been derived.<br><br>Thus we have found that the differential of ''x''<sup>2</sup> is 2''xdx'', therefore, if we have given 2''xdx'', we know that it must have been derived from ''x'', or plus a constant term.<br><br>(292.) '''The function from which the given differential has been derived, is called its ''integral''.''' Hence, as we are not certain whether the integral has a constant quantity or not added to it, we annex a constant quantity represented by C, the value of which is to be determined from the nature of the problem. <br><br>(293.) Leibnitz considered the differentials of functions as indefinitely small differences, and the sum of these indefinitely small differences he regarded as making up the function; hence the letter S was placed before the differential to show that the sum was to be taken. As it was frequently required to place S before a compound expression, it was elongated into the sign ''∫'', which, being placed before a differential, denotes that its integral is to be taken. Thus,<br><center><math>\int 2xdx = x^2+C</math>.</center>This sign ''∫'' is still retained ever by those whu reject the philosophy of Leibnitz. |''Elements of Analytical Geometry and of The Differential and Integral Calculus'', Integral Calculus, Section I}} |
|
{{from|1=A<span style{{=}}"font-size: 70%;>RTICLE</span> (291.) T<span style{{=}}"font-size: 70%;>HE</span> Integral Calculus is the reverse of the Differential Calculus, its object being to determine the expression or function from which a given differential has been derived.<br><br>Thus we have found that the differential of ''x''<sup>2</sup> is 2''xdx'', therefore, if we have given 2''xdx'', we know that it must have been derived from ''x'', or plus a constant term.<br><br>(292.) '''The function from which the given differential has been derived, is called its ''integral''.''' Hence, as we are not certain whether the integral has a constant quantity or not added to it, we annex a constant quantity represented by C, the value of which is to be determined from the nature of the problem. <br><br>(293.) Leibnitz considered the differentials of functions as indefinitely small differences, and the sum of these indefinitely small differences he regarded as making up the function; hence the letter S was placed before the differential to show that the sum was to be taken. As it was frequently required to place S before a compound expression, it was elongated into the sign ''∫'', which, being placed before a differential, denotes that its integral is to be taken. Thus,<br><div style="text-align: center;"><math>\int 2xdx = x^2+C</math>.</div>This sign ''∫'' is still retained ever by those whu reject the philosophy of Leibnitz. |2=''Elements of Analytical Geometry and of The Differential and Integral Calculus'', Integral Calculus, Section I, Integration of Monomial Differentials}} |
|
|
|
|
|
实际上,书中的积分号仅仅写作<span style="font-family:serif;">''∫''</span>,没有写得像今天的<math>\int</math>那么长。 |
|
实际上,书中的积分号仅仅写作<span style="font-family:serif;">''∫''</span>,没有写得像今天的<math>\int</math>那么长。 |
|
|
|
|
|
<center>[[File:Elements of Analytical Geometry and of The Differential and Integral Calculus.pdf|page=228|300px]]</center> |
|
<div style="text-align: center;">[[File:Elements of Analytical Geometry and of The Differential and Integral Calculus.pdf|page=228|300px]]</div> |
|
</tabber> |
|
</tabber> |
|
|
|
|