欢迎来到奇葩栖息地!欢迎加入Discord服务器:XfrfHCzfbW。欢迎加入QQ频道:r01m9y3iz6。请先至特殊:参数设置验证邮箱后再进行编辑。在特殊:参数设置挑选自己想要使用的小工具!不会编辑?请至这里学习Wikitext语法。
物竞小黑板:修订间差异
Microcandela(讨论 | 贡献) 小无编辑摘要 |
Microcandela(讨论 | 贡献) 无编辑摘要 |
||
| (未显示3个用户的28个中间版本) | |||
| 第1行: | 第1行: | ||
这是一个菜狗创建的页面,目的是为了帮助大家热爱物理竞赛,欢迎大家一起编辑,也请大家帮助指出其中的错误。请各位在'''''讨论'''''中提出认为需要改进的地方。 |
|||
==简介== |
|||
== “高考易错题” == |
|||
这是一个菜{{Heimu|不是蔡}}鸡创建的页面,目的是为了帮助大家热爱物理竞赛,欢迎大家一起编辑,也请大家帮助指出其中的错误。 |
|||
谈到高考易错题,大多数人想到的是学生容易做错的题目。但我们这里讨论一些'''老师容易出错'''的题目。 |
|||
==“高考易错题”== |
|||
=== 例1 === |
|||
[[文件:Physicsblackboard1.jpg|thumb|例1-图1]] |
|||
''在一个光滑水平面上有一孔,中间穿过一根轻绳,桌面上的一段连接一个质量为<math>m</math>的球,桌面下的一段连接两个质量为<math>m</math>的球,桌面上绳长初态为<math>l</math>。桌面上的球以切向速度<math>v_0=\sqrt{gl}</math>绕孔做圆周运动。现在释放绳,问桌面上绳最短为多长?'' |
|||
我们设桌面上的绳缩短量为<math>x</math>,则我们需要算出<math>x_\rm{max}</math>的值。 |
|||
如果这题被老师一时兴起出到高考试卷上,那么解题过程应该是这样的: |
|||
由能量守恒:<math>\frac{1}{2}mv_0^2 = \frac{1}{2}mv_1^2 - 2mgx</math> ① |
|||
由牛顿第二定律:<math>\frac{mv_1^2}{l - x} = 2mg</math> ② |
|||
然而这样做是不对的。这里默认了<math>x_\rm{max}</math>时沿绳方向的加速度只有向心加速度。事实上,此时沿绳不止有向心加速度,桌面下方的<math>2m</math>会再次上升,原因在最后会解释。 |
|||
那我们怎样解决这个问题呢?我们可以使用角动量。 |
|||
由<math>\vec{F} = m \vec{a}</math>: |
|||
<math>\vec{r} \times \vec{F} \cdot \Delta t = \vec{r} \times m \vec{a} \cdot \Delta t</math> |
|||
<math>\vec{M} \cdot \Delta t = \vec{r} \times m \Delta \vec{v}</math> |
|||
又<math> \Delta (\vec{r} \times m \vec{v})</math> |
|||
<math> = \Delta \vec{r} \times m \vec{v} + \vec{r} \times \Delta (m \vec{v})</math> |
|||
<math> = \vec{v} \cdot \Delta t \times m \vec{v} + \vec{r} \times m \Delta \vec{v}</math> |
|||
<math> = 0 + \vec{r} \times m \Delta \vec{v}</math> |
|||
所以<math>\vec{M} \cdot \Delta t = \Delta (\vec{r} \times m \vec{v})</math> |
|||
记作<math>\vec{H} = \Delta \vec{L}</math> |
|||
其中,<math>\vec{H}</math>是角冲量,<math>\vec{L}</math>是角动量。 |
|||
在此题中,使用角动量是好的。因为桌面上的小球受到绳的力是有心力,即:若选孔为支点,则运动过程中绳上拉力力臂始终为0,力矩为0,角动量守恒。 |
|||
由此,得方程:<math>m v_0 l = m v_1 (l-x)</math> ③ |
|||
联立①③,得<math>x_\rm{max}=\frac{7-\sqrt{17}}{8}</math><math>l</math> |
|||
由这个结果不难发现,<math>x_\rm{max}</math>时,向心加速度为<math>\frac{-13+5\sqrt{17}}{2}g >2g</math>,说明我们之前的想法是正确的。 |
|||
这个问题就轻松而愉快地解决了! |
|||
== 一点数学 == |
|||
===几何法(一)=== |
|||
''设<math>x < R</math> , 求<math> \int_{0}^{\pi} \frac{\sin^3 \theta}{(x^2+R^2-2xR \cos \theta)^{\frac{3}{2}}}\,\textup{d}\theta</math>'' |
|||
''答案:<math>\frac{4}{3R^3}</math> |
|||
本题的常规解法是将分子上的一个<math>\sin\theta</math>放进<math>\textup{d}\theta</math>里,以<math>\cos\theta</math>为变元进行积分。然而这样的积分还需进行繁杂的换元操作,计算起来煞费功夫。 |
|||
然而我们进行一些观察就能得到一些“巧妙”的细节:从题面入手,分母是齐次式,并且具有余弦定理的形式;从答案入手,答案中竟然不含<math>x</math>,又可以发现<math>\frac{4}{3}=\int_{0}^{\pi} \sin^3 \theta\,\textup{d}\theta</math>。这一切似乎都在将我们引向一个更好的解法:几何法。 |
|||
[[文件:Physicsblackboard2.png|thumb|例2-图1]] |
|||
各量的意义已在图中标明。 |
|||
由余弦定理,不难得出<math>l=\sqrt{x^2+R^2-2xR \cos \theta}</math> |
|||
由正弦定理,不难得出<math>\frac{\sin\theta}{l}=\frac{\sin\varphi}{R}=\frac{\sin\alpha}{x}</math> |
|||
由图中的几何关系,<math>\textup{d}\theta=\textup{d}\varphi-\textup{d}\alpha</math> |
|||
考虑到<math>x < R</math>的条件下,<math>\theta :0 \rightarrow \frac{\pi}{2}</math>的过程对应<math>\varphi :0 \rightarrow \frac{\pi}{2}</math>和<math>\alpha :0 \rightarrow 0</math> |
|||
于是有<math> \int_{0}^{\pi} \frac{\sin^3 \theta}{(x^2+R^2-2xR \cos \theta)^{\frac{3}{2}}}\,\textup{d}\theta = \int_{0}^{\pi} \frac{\sin^3 \theta}{(x^2+R^2-2xR \cos \theta)^{\frac{3}{2}}}\,\textup{d}\varphi - \int_{0}^{0} \frac{\sin^3 \theta}{(x^2+R^2-2xR \cos \theta)^{\frac{3}{2}}}\,\textup{d}\alpha</math> |
|||
<math> = \int_{0}^{\pi} \frac{\sin^3 \varphi}{R^3}\,\textup{d}\varphi - \int_{0}^{0} \frac{\sin^3 \alpha}{x^3}\,\textup{d}\alpha </math> |
|||
<math>=\frac{4}{3R^3} </math> |
|||
我们可以自然地由几何得到,这个积分的结果和<math>x</math>与<math>R</math>的大小关系有关。 |
|||
[[用户:Microcandela|Microcandela]]([[用户讨论:Microcandela|留言]])于2024年4月独立得出以上结果。 |
|||
[[用户:Microcandela|Microcandela]]([[用户讨论:Microcandela|留言]]) 2024年5月11日 (六) 15:42 (UTC) 时隔3年,再度编写此条目。 |
|||
===几何法(二)=== |
|||
''将许多石块以相同的速度大小<math>v_{0}</math>,不同的发射角<math>\theta</math>从地面上<math>(0,0)</math>点抛出,石块在重力的作用下会以抛物线轨道运动,它们与地面发生完全非弹性碰撞,碰到地面后立刻停止运动。求在同一竖直面内各抛物线轨道离原点最远点所组成的曲线的方程。'' |
|||
本题可以通过正常的代数解法解出答案,但将面临繁琐的三角函数运算化简,并且需要借助“惊人的注意力”。事实上,当我们进行几步简单的运算后,便可发现一些直线间的斜率关系,启示我们向几何法靠近。 |
|||
首先进行几步初步的运算: |
|||
<math>\begin{cases} x=v_{0} t \cos\theta \\ y=v_{0} t \sin\theta - \frac{1}{2} g t^{2} \end{cases}</math> |
|||
<math>\Rightarrow t=\frac{x}{v_{0} \cos \theta}</math> |
|||
<math>\Rightarrow y=x \tan \theta-\frac{g x^{2}}{2v_{0}^{2}} (1+\tan ^{2} \theta)</math> |
|||
<math>\Rightarrow</math>顶点<math>(\frac{v_{0}^{2} \sin \theta \cos \theta}{g} , \frac{v_{0}^{2} \sin ^{2}theta}{2g})</math> |
|||
《力学篇 程稼夫》就已经指出,最远点满足条件<math>\vec{r} \cdot \vec{v}=0</math>即<math>\frac{y}{x} \cdot \frac{v_{y}}{v_{x}} = -1</math> |
|||
<math>\Rightarrow \frac{v_{0} t \sin\theta - \frac{1}{2} g t^{2}}{v_{0} t \cos\theta} \cdot \frac{v_{0} \sin\theta - g t}{v_{0} \cos\theta } = -1</math> |
|||
<math>\frac{1}{2} (g t)^{2} -\frac{3}{2} v_{0} \sin \theta \cdot g t +v_{0}^{2} = 0</math> |
|||
将<math>g t</math>看作变元,需满足<math>\Delta = \frac{9}{4} v_{0}^{2} \sin ^{2} \theta – 2 v_{0}^{2}\geq 0</math> |
|||
{{study}} |
|||
[[分类:物理]] |
|||
2024年5月12日 (日) 07:13的最新版本
这是一个菜狗创建的页面,目的是为了帮助大家热爱物理竞赛,欢迎大家一起编辑,也请大家帮助指出其中的错误。请各位在讨论中提出认为需要改进的地方。
“高考易错题”
谈到高考易错题,大多数人想到的是学生容易做错的题目。但我们这里讨论一些老师容易出错的题目。
例1
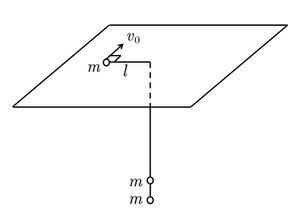
在一个光滑水平面上有一孔,中间穿过一根轻绳,桌面上的一段连接一个质量为[math]\displaystyle{ m }[/math]的球,桌面下的一段连接两个质量为[math]\displaystyle{ m }[/math]的球,桌面上绳长初态为[math]\displaystyle{ l }[/math]。桌面上的球以切向速度[math]\displaystyle{ v_0=\sqrt{gl} }[/math]绕孔做圆周运动。现在释放绳,问桌面上绳最短为多长?
我们设桌面上的绳缩短量为[math]\displaystyle{ x }[/math],则我们需要算出[math]\displaystyle{ x_\rm{max} }[/math]的值。
如果这题被老师一时兴起出到高考试卷上,那么解题过程应该是这样的:
由能量守恒:[math]\displaystyle{ \frac{1}{2}mv_0^2 = \frac{1}{2}mv_1^2 - 2mgx }[/math] ①
由牛顿第二定律:[math]\displaystyle{ \frac{mv_1^2}{l - x} = 2mg }[/math] ②
然而这样做是不对的。这里默认了[math]\displaystyle{ x_\rm{max} }[/math]时沿绳方向的加速度只有向心加速度。事实上,此时沿绳不止有向心加速度,桌面下方的[math]\displaystyle{ 2m }[/math]会再次上升,原因在最后会解释。
那我们怎样解决这个问题呢?我们可以使用角动量。
由[math]\displaystyle{ \vec{F} = m \vec{a} }[/math]:
[math]\displaystyle{ \vec{r} \times \vec{F} \cdot \Delta t = \vec{r} \times m \vec{a} \cdot \Delta t }[/math]
[math]\displaystyle{ \vec{M} \cdot \Delta t = \vec{r} \times m \Delta \vec{v} }[/math]
又[math]\displaystyle{ \Delta (\vec{r} \times m \vec{v}) }[/math]
[math]\displaystyle{ = \Delta \vec{r} \times m \vec{v} + \vec{r} \times \Delta (m \vec{v}) }[/math]
[math]\displaystyle{ = \vec{v} \cdot \Delta t \times m \vec{v} + \vec{r} \times m \Delta \vec{v} }[/math]
[math]\displaystyle{ = 0 + \vec{r} \times m \Delta \vec{v} }[/math]
所以[math]\displaystyle{ \vec{M} \cdot \Delta t = \Delta (\vec{r} \times m \vec{v}) }[/math]
记作[math]\displaystyle{ \vec{H} = \Delta \vec{L} }[/math]
其中,[math]\displaystyle{ \vec{H} }[/math]是角冲量,[math]\displaystyle{ \vec{L} }[/math]是角动量。
在此题中,使用角动量是好的。因为桌面上的小球受到绳的力是有心力,即:若选孔为支点,则运动过程中绳上拉力力臂始终为0,力矩为0,角动量守恒。
由此,得方程:[math]\displaystyle{ m v_0 l = m v_1 (l-x) }[/math] ③
联立①③,得[math]\displaystyle{ x_\rm{max}=\frac{7-\sqrt{17}}{8} }[/math][math]\displaystyle{ l }[/math]
由这个结果不难发现,[math]\displaystyle{ x_\rm{max} }[/math]时,向心加速度为[math]\displaystyle{ \frac{-13+5\sqrt{17}}{2}g \gt 2g }[/math],说明我们之前的想法是正确的。
这个问题就轻松而愉快地解决了!
一点数学
几何法(一)
设[math]\displaystyle{ x \lt R }[/math] , 求[math]\displaystyle{ \int_{0}^{\pi} \frac{\sin^3 \theta}{(x^2+R^2-2xR \cos \theta)^{\frac{3}{2}}}\,\textup{d}\theta }[/math]
答案:[math]\displaystyle{ \frac{4}{3R^3} }[/math]
本题的常规解法是将分子上的一个[math]\displaystyle{ \sin\theta }[/math]放进[math]\displaystyle{ \textup{d}\theta }[/math]里,以[math]\displaystyle{ \cos\theta }[/math]为变元进行积分。然而这样的积分还需进行繁杂的换元操作,计算起来煞费功夫。
然而我们进行一些观察就能得到一些“巧妙”的细节:从题面入手,分母是齐次式,并且具有余弦定理的形式;从答案入手,答案中竟然不含[math]\displaystyle{ x }[/math],又可以发现[math]\displaystyle{ \frac{4}{3}=\int_{0}^{\pi} \sin^3 \theta\,\textup{d}\theta }[/math]。这一切似乎都在将我们引向一个更好的解法:几何法。
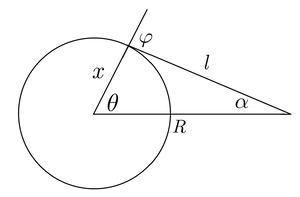
各量的意义已在图中标明。
由余弦定理,不难得出[math]\displaystyle{ l=\sqrt{x^2+R^2-2xR \cos \theta} }[/math]
由正弦定理,不难得出[math]\displaystyle{ \frac{\sin\theta}{l}=\frac{\sin\varphi}{R}=\frac{\sin\alpha}{x} }[/math]
由图中的几何关系,[math]\displaystyle{ \textup{d}\theta=\textup{d}\varphi-\textup{d}\alpha }[/math]
考虑到[math]\displaystyle{ x \lt R }[/math]的条件下,[math]\displaystyle{ \theta :0 \rightarrow \frac{\pi}{2} }[/math]的过程对应[math]\displaystyle{ \varphi :0 \rightarrow \frac{\pi}{2} }[/math]和[math]\displaystyle{ \alpha :0 \rightarrow 0 }[/math]
于是有[math]\displaystyle{ \int_{0}^{\pi} \frac{\sin^3 \theta}{(x^2+R^2-2xR \cos \theta)^{\frac{3}{2}}}\,\textup{d}\theta = \int_{0}^{\pi} \frac{\sin^3 \theta}{(x^2+R^2-2xR \cos \theta)^{\frac{3}{2}}}\,\textup{d}\varphi - \int_{0}^{0} \frac{\sin^3 \theta}{(x^2+R^2-2xR \cos \theta)^{\frac{3}{2}}}\,\textup{d}\alpha }[/math]
[math]\displaystyle{ = \int_{0}^{\pi} \frac{\sin^3 \varphi}{R^3}\,\textup{d}\varphi - \int_{0}^{0} \frac{\sin^3 \alpha}{x^3}\,\textup{d}\alpha }[/math]
[math]\displaystyle{ =\frac{4}{3R^3} }[/math]
我们可以自然地由几何得到,这个积分的结果和[math]\displaystyle{ x }[/math]与[math]\displaystyle{ R }[/math]的大小关系有关。
Microcandela(留言)于2024年4月独立得出以上结果。
Microcandela(留言) 2024年5月11日 (六) 15:42 (UTC) 时隔3年,再度编写此条目。
几何法(二)
将许多石块以相同的速度大小[math]\displaystyle{ v_{0} }[/math],不同的发射角[math]\displaystyle{ \theta }[/math]从地面上[math]\displaystyle{ (0,0) }[/math]点抛出,石块在重力的作用下会以抛物线轨道运动,它们与地面发生完全非弹性碰撞,碰到地面后立刻停止运动。求在同一竖直面内各抛物线轨道离原点最远点所组成的曲线的方程。
本题可以通过正常的代数解法解出答案,但将面临繁琐的三角函数运算化简,并且需要借助“惊人的注意力”。事实上,当我们进行几步简单的运算后,便可发现一些直线间的斜率关系,启示我们向几何法靠近。
首先进行几步初步的运算:
[math]\displaystyle{ \begin{cases} x=v_{0} t \cos\theta \\ y=v_{0} t \sin\theta - \frac{1}{2} g t^{2} \end{cases} }[/math]
[math]\displaystyle{ \Rightarrow t=\frac{x}{v_{0} \cos \theta} }[/math]
[math]\displaystyle{ \Rightarrow y=x \tan \theta-\frac{g x^{2}}{2v_{0}^{2}} (1+\tan ^{2} \theta) }[/math]
[math]\displaystyle{ \Rightarrow }[/math]顶点[math]\displaystyle{ (\frac{v_{0}^{2} \sin \theta \cos \theta}{g} , \frac{v_{0}^{2} \sin ^{2}theta}{2g}) }[/math]
《力学篇 程稼夫》就已经指出,最远点满足条件[math]\displaystyle{ \vec{r} \cdot \vec{v}=0 }[/math]即[math]\displaystyle{ \frac{y}{x} \cdot \frac{v_{y}}{v_{x}} = -1 }[/math]
[math]\displaystyle{ \Rightarrow \frac{v_{0} t \sin\theta - \frac{1}{2} g t^{2}}{v_{0} t \cos\theta} \cdot \frac{v_{0} \sin\theta - g t}{v_{0} \cos\theta } = -1 }[/math]
[math]\displaystyle{ \frac{1}{2} (g t)^{2} -\frac{3}{2} v_{0} \sin \theta \cdot g t +v_{0}^{2} = 0 }[/math]
将[math]\displaystyle{ g t }[/math]看作变元,需满足[math]\displaystyle{ \Delta = \frac{9}{4} v_{0}^{2} \sin ^{2} \theta – 2 v_{0}^{2}\geq 0 }[/math]
| 数学 |
| ||||
|---|---|---|---|---|---|
| 物理 |
| ||||
| 化学 |
| ||||
| 信息学 |
| ||||
| 生物学 |
| ||||
| 其他 | |||||
