第149行:
第149行:
| 癸
| 癸
! {{lang|el|Κ}}
! {{lang|el|Κ}}
| {{ruby|𠯆|nǔ}}
| {{ruby|𠯆|nǚ }}
! {{lang|el|κ}}
! {{lang|el|κ}}
| 女
| 女
2024年3月10日 (日) 07:09的版本
这些公式被包含在<math>(包括$或\(\)及不换行的\[\]) 或<chem>标签中,请稍等片刻等待前端渲染 。E X,请参见帮助:数学公式 。
“
米利堅羅密士譔,英國偉烈亞力口譯,海寧李善蘭筆述。
”
——《代微積拾級》
《代微积拾( shè ) 级》 ,由英国汉学家、来华传教士伟烈亚力 (Alexander Wylie,1815年4月6日-1887年2月10日)口译,清代数学家李善兰 (1811年1月22日-1882年12月9日)笔述;1859年由上海墨海书馆 (The London Missionary Society Press)出版。原著为美国数学家伊莱亚斯·罗密士 (Elias Loomis,1811年8月7日-1889年8月15日)于1851年出版的《解析几何和微积分初步》(Elements of Analytical Geometry and of The Differential and Integral Calculus ) 。
据考证,李善兰翻译所用的底本,应为1852年再版的版本,而非1851年的初版(内容差别较大)。原著在1874年改版,在此之前有不下20个版次(包括1856年的第6版、1859年的第10版、1864年的第17版、1868年的第19版等),畅销程度可见一斑。
1872年(明治5年),这本书被福田半译至日文,但书中并未使用李善兰创立的对应符号系统(参见#符号 ),而是使用原著的符号。
需要注意的是,这本书中的定义以今天的眼光来看并不严谨。一方面,当时的微积分学基础并不牢固,(ε, δ)-极限定义还未出现,书中仍然只使用未严格定义的无穷小量来定义概念;另一方面,这本书本身就是入门教材,不应过于晦涩难懂。
作者 李善蘭,字壬叔,海寧人。諸生。從陳奐受經,於算術好之獨深。 十歲即通九章,後得測圓海鏡、句股割圜記,學益進。疑割圜法非自然,精思得其理。嘗謂道有一貫,藝亦然。測圓海鏡每題皆有法有草,法者,本題之法也;草者,用立天元一曲折以求本題之法,乃造法之法,法之源也。算術大至躔離交食,細至米鹽瑣碎,其法至繁,以立天元一演之,莫不能得其法。故立天元一者,算學中之一貫也。並時明算如錢塘戴煦,南匯張文虎,烏程徐有壬、汪曰楨,歸安張福僖,皆相友善。咸豐初,客上海,識英吉利偉烈亞力、艾約瑟、韋廉臣三人,偉烈亞力精天算,通華言。善蘭以歐幾里幾何原本十三卷、續二卷,明時譯得六卷,因與偉烈亞力同譯後九卷,西士精通幾何者尟,其第十卷尤玄奧,未易解,譌奪甚多,善蘭筆受時,輒以意匡補。譯成,偉烈亞力歎曰:「西士他日欲得善本,當求諸中國也!」偉烈亞力又言美國天算名家羅密士嘗取代數、微分、積分合為一書,分款設題,較若列眉,復與善蘭同譯之,名曰代微積拾級十八卷。代數變天元、四元,別為新法,微分、積分二術,又藉徑於代數,實中土未有之奇秘。善蘭隨體剖析自然,得力於海鏡為多。 [取自《清史稿·列傳二百九十四·疇人二》]
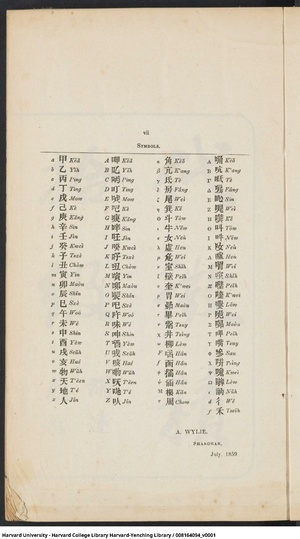
影印本 符号 字母 符号表,注意希腊字母Ρ 与Μ 对应颠倒 在书中,小写拉丁字母 以天干(10个)、地支(12个)和物(w)、天(x)、地(y)、人(z)对应;小写希腊字母 以二十八宿 的前24个对应。大写字母将小写字母对应的汉字左侧加上“口”来表示,即使加上口字旁的字已存在,也按照小写的读音来读(例如小写的v对应“亥”,那么大写的V对应的“咳”也读作hài)。另外还有一些专用的符号单独对应。
符号对照表
A
呷( jiǎ )
a
甲
Α
唃( jiǎo )
α
角( jiǎo )
F
㖤( hán )
B
𠮙( yǐ ) b
乙
Β
吭( kàng )
β
亢( kàng )
f
函
C
𠰳( bǐng ) c
丙
Γ
呧( dǐ )
γ
氐( dǐ )
ϕ
𭡝( hán )
D
叮
d
丁
Δ
δ
房
ψ
涵
E
𱒐( wù ) e
戊
Ε
吣( xīn )
M
根
F
𠯇( jǐ ) f
己
Ζ
𠳿( wěi )
ζ
尾
π
周[表注 1]
G
𱓒( gēng ) g
庚
Η
𱕍( jī ) η
箕( jī )
ε
訥( nè ) (讷)[表注 2]
H
㖕( xīn ) h
辛
Θ
呌( dǒu )
θ
斗( dǒu )
d
彳( wēi ) [表注 3]
I
𠰃( rén ) i
壬
Ι
吽( níu )
ι
牛
∫
禾( jī ) [表注 4]
J
𱓩( guǐ ) j
癸
Κ
𠯆( nǚ )
κ
女
K
吇( zǐ )
k
子
Λ
嘘( xū )
λ
虛
L
吜( choǔ )
l
丑
Μ
𠱓( wēi ) [表注 5] μ
危
M
𠻤( yín ) m
寅
Ν
㗌( shì ) ν
室
N
𠰭( mǎo ) n
卯
Ξ
ξ
壁
O
㖘( chén )
o
辰
Ο
喹( kuí )
ο
奎
P
𱒄( sì ) p
巳
Π
嘍( lóu ) (喽)
Q
吘( wǔ )
q
午
Ρ
喟( wèi ) [表注 6] ρ
胃
R
味
r
未
Σ
𭈾( mǎo ) σ
昴( mǎo )
S
呻
s
申
Τ
嗶( bì ) (哔)
τ
畢(毕)
T
唒( yǒu )
t
酉
Υ
嘴( zī )
υ
觜( zī )
U
㖅( xù ) u
戌
Φ
嘇( shēn ) (𰇼 )
V
咳( hài )
v
亥
Χ
𠯤( jǐn ) χ
井
W
𭈘( wù ) w
物
Ψ
𠺌( guǐ )
X
𱒆( tiān ) x
天
Ω
ω
柳
Y
哋( dì )
y
地
Z
㕥( rén ) z
人
运算符及其他引进符号
LaTeX
HTML
说明
[math]\displaystyle{ \bot }[/math] [表注 7] ⊥[表注 8]
正也,加也[表注 9]
[math]\displaystyle{ \top }[/math] [表注 10] ⊤[表注 11]
負也,減也[表注 12]
[math]\displaystyle{ \times }[/math] [表注 13] ×[表注 14]
相乘也
[math]\displaystyle{ \div }[/math] [表注 15] ÷[表注 16]
約也,或作[math]\displaystyle{ - }[/math]
[math]\displaystyle{ :::: }[/math]
::::
四率比例也
[math]\displaystyle{ () }[/math]
()
括諸數為一數也,名曰括弧
[math]\displaystyle{ \sqrt{} }[/math] [表注 17] √
開方根也
[math]\displaystyle{ = }[/math]
=
等於[表注 18]
[math]\displaystyle{ \lt }[/math]
<
右大於左
[math]\displaystyle{ \gt }[/math]
>
左大於右
[math]\displaystyle{ 0 }[/math]
0
無也
[math]\displaystyle{ \infty }[/math] [表注 19] ∞
無窮也
注释
↑ 指圆周率 。
↑ 指自然常数 ,疑似应为e。
↑ 音同“微”,指微分号。
↑ 音同“积”,指积分号。
↑ 书中表格与Ρ 颠倒。
↑ 书中表格与Μ 颠倒。
↑ \bot
↑ U+22A5,⊥⊥⊥⊥⊥
↑ 此处并非垂直符号[math]\displaystyle{ \perp }[/math] (\perp)或⟂(U+27C2,⟂)。不使用加号+(U+002B,&#plus;+)是因为易与汉字数字“十”混淆。此为“上”的古字(丄,U+4E04,丄)。
↑ \top
↑ U+22A4,⊤⊤⊤
↑ 不使用减号−(U+2212,−−)或连字暨减号-(U+002D,-)是因为易与汉字数字“一”混淆。此为“下”的古字(丅,U+4E05,丅 )。
↑ \times
↑ U+00D7,××
↑ \div
↑ U+00F7,÷÷
↑ \sqrt{}
↑ 与原符号不同,书中为防止与汉字数字“二”混淆而被拉长。
↑ \infty
术语 书中新创了大量术语,其中有很多沿用至今。
术语表
原文
译文
Abbreviated expression
簡式
Abscissa
橫線
Acute angle
銳角
Add
加
Addition
加法
Adjacent angle
旁角
Algebra
代數學
Algebra curve
代數曲線
Altitude
高,股,中垂線
Anomaly
奇式
Answer
答
Antecedent
前率( shuài )
Approximation
迷率
Arc
弧
Area
面積
Arithmetic
數學
Asymptote
漸近線
Axiom
公論
Axis
軸,軸線
Axis major
長徑,長軸
Axis minor
短徑,短軸
Axis of abscissas
橫軸
Axis of coordinates
總橫軸
Axis of ordinate
縱軸
Base
底,勾
Binominal
二項式
Binomial theorem
合名法
Biquadratic parabola
三乘方拋物線
Bisect
平分
Brackets
括弧
Center of an ellipse
中點
Chord
通弦
Circle
平圜
Circular expression
圜式
Circumference
周
Circumsoribed
外切
Coefficient
係數
Common algebra expression
代數常式
Coincide
合
Commensurable
有等數
Common
公
Complement
餘
Complementary angle
餘角
Concave
凹
Concentric
同心
Cone
圓錐
Conjugate axis
相屬軸
Conjugate diameter
相屬徑
Conjugate hyperbola
相屬雙曲線
Consequent
後率
Constant
常數
Construct
做圖
Contact
切
Converging series
斂級數
Convex
凸
Coordinates
總橫線
Corollary
系
Cosecant
餘割
Cosine
餘弦
Cotangent
餘切
Coversedsine
餘矢
Cube
立方
Cube root
立方根
Cubical parabola
立方根拋物線
Curvature
曲率
Curve
曲線
Cusp
歧點
Cycloid
擺線
Cylinder
圜柱
Decagon
十邊形
Decrease
損
Decreasing function
損函數
Definition
界說
Degree of an expression
次
Degree of angular measurement
度
Denominator
分母,母數
Dependent variable
因變數
Diagonal
對角線
Diameter
徑
Difference
較
Differential
微分
Differential calculus
微分學
Differential coefficient
微係數
Differentiate
求微分
Direction
方向
Directrix
準線
Distance
距線
Diverging lines
漸遠線
Diverging series
發級數
Divide
約
Dividend
實
Division (absolute)
約法
Division (concrete)
除法
Divisor
法
Dodecahedron
十二面體
Duplicate
倍比例
Edge of polyhedron
稜
Ellipse
橢圓
Equal
等
Equation
方程式
Equation of condition
偶方程式
Equiangular
等角
Equilateral
等邊
Equimultiple
等倍數
Evolute
漸申線
Evolution
開方
Expand
詳
Expansion
詳式
Explicit function
陽函數
Exponent
指數
Expression
式
Extreme and mean ratio
中末比例
Extremes of a proportion
首尾二率
Face
面
Factor
乘數
Figure
行、圖
Focus of a conic section
心
Formula
法
Fourth proportional
四率
Fraction
分
Fractional expression
分式
Frustum
截圜錐
Function
函數
General expression
公式
Generate
生
Generating circle
母輪
Generating point
母點
Geometry
幾何學
Given ratio
定率
Great circle
大圈
Greater
大
Hemisphere
半球
Hendecagon
十一邊形
Heptagon
七邊形
Hexagon
六邊形
Hexahedron
六面體
Homogeneous
同類
Homologous
相當
Hypoerbola
雙曲線,雙線
Hyperbolic spiral
雙線螺旋
Hypotheneuse
弦
Icosahedron
二十面體
Implicit function
陰函數
Impossible expression
不能式
Inclination
倚度
Incommensurable
無等數
Increase
增
Increasing function
增函數
Increment
長數
Indefinite
無定
Independent variable
自變數
Indeterminate
未定
Infinite
無窮
Inscribed
內切,所容
Integral
積分
Integral calculus
積分學
Integrate
求積分
Interior
裏
Intersect
交
Intersect at right angles
正交
Inverse circular expression
反圜式
Inverse proportion
反比例
Irrational
無比例
Isolated point
特點
Isosceles triangle
二等邊三角形
Join
聯
Known
已知
Law of continuity
漸變之理
Leg of an angle
夾角邊
Lemma
例
Length
長短
Less
小
Limits
限
Limited
有限
Line
線
Logarithm
對數
Logarithmic curve
對數曲線
Logarithmic spiral
對數螺線
Lowest term
最小率
Maximum
極大
Mean proportion
中率
Means
中二率
Measure
度
Meet
遇
Minimum
極小
Modulus
對數根
Monomial
一項式
Multinomial
多項式
Multiple
倍數
Multiple point
倍點
Multiplicand
實
Multiplication
乘法
Multiplier
法
Multiply
乘
Negative
負
Nonagon
九邊形
Normal
法線
Notation
命位,紀法
Number
數
Numerator
分子,子數
Oblique
斜
Obtuse
鈍
Octagon
八邊形
Octahedron
八面體
Opposite
對
Ordinate
縱線
Origin of coordinate
原點
Parabola
拋物線
Parallel
平行
Parallelogram
平行邊形
Parallelepiped
立方體
Parameter
通徑
Part
分,段
Partial differential
偏微分
Partial differential coefficient
偏微係數
Particular case
私式
Pentagon
五邊形
Perpendicular
垂線,股
Plane
平面
Point
點
Point of contact
切點
Point of inflection
彎點
Point of intersection
交點
Polar curve
極曲線
Polar distance
極距
Pole
極
Polygon
多邊形
Polyhedron
多面體
Polynomial
多項式
Positive
正
Postulate
求
Power
方
Primitive axis
舊軸
Problem
題
Produce
引長
Product
得數
Proportion
比例
Proposition
款
Quadrant
象限
Quadrilateral figure
四邊形
Quadrinomial
四項式
Quam proxime
任近
Quantity
幾何
Question
問
Quindecagon
十五邊形
Quotient
得數
Radius
半徑
Radius vector
帶徑
Ratio
率
Rational expression
有比例式
Reciprocal
交互
Rectangle
矩形
Rectangular
正
Reduce
化
Reduce to a simple form
相消
Regular
正
Relation
連屬之理
Represent
顯
Reverse
相反
Revolution
匝
Right angle
直角
Right-angled triangle
勾股形
Round
圜
Root
根
Root of equation
滅數
Scalene triangle
不等邊三角形
Scholium
案
Secant
割線
Secant (trigonometrical)
正割
Segment
截段
Semicircle
半圜周
Semicubical parabola
半立方拋物線
Semibiquadratic parabola
半三乘方拋物線
Series
級數
Sextant
記限
Side
邊
Sign
號
Similar
相似
Sine
正弦
Singular point
獨異點
Smaller
少
Solid
體
Solidity
體積
Sphere
立圜體,球
Spiral
螺線
Spiral of archimedes
亞奇默德螺線
Square
方,正方,冪
Square root
平方根
Straight line
直線
Subnormal
次法線
Subtangent
次切線
Subtract
減
Subtraction
減法
Sum
和
Supplement
外角
Supplementary chord
餘通弦
Surface
面
Surface of revolution
曲面積
Symbol of quantity
元
Table
表
Tangent
切線
Tangent (trigonometrical)
正切
Term of an expression
項
Term of ratio
率
Tetrahedron
四面體
Theorem
術
Total differential
全微分
Transcendental curve
越曲線
Transcendental expression
越式
Transcendental function
越函數
Transform
易
Transverse axis
橫軸,橫徑
Trapezoid
二平行邊四邊形
Triangle
三角形
Trident
三齒線
Trigonometry
三角法
Trinomial
三項式
Triplicate
三倍
Trisection
三等分
Unequal
不等
Unit
一
Unknown
未知
Unlimited
無線
Value
同數
Variable
變數
Variation
變
Verification
證
Versedsine
正矢
Vertex
頂點
Vertical plane
縱面
函数 在卷十的开头,可以看到那句经典名句:
微分之數有二,一曰常數,一曰變數;變數以天地人物等字代之,常數以甲乙子丑等字代之。[math]\displaystyle{ 地\xlongequal{\qquad}甲天\bot乙 }[/math] ,則線之甲與乙,俱僅有一同數任在何點永不變,而天與地之同數則每點皆變也。凡此變數中函彼變數,則此爲彼之函數。 [math]\displaystyle{ 地\xlongequal{\qquad}甲天\bot乙 }[/math] ,則地爲天之函數;又平圜之式爲[math]\displaystyle{ 地\xlongequal{\qquad}\sqrt{味^二\top甲^二} }[/math] ,味爲半徑,天爲正弦,地爲餘弦;橢圓之式爲[math]\displaystyle{ 地\xlongequal{\qquad} }[/math] 呷 / 𠮙 [math]\displaystyle{ \sqrt{二呷天\top天^二} }[/math] ,皆地爲天之函數也。[math]\displaystyle{ 天\xlongequal{\qquad}函(地) \ 地\xlongequal{\qquad}函(天) }[/math] ,此天爲地之函數,亦地爲天之函數。[取自《代微積拾級·卷十 微分一·例》]
原文如下:
Elements of Analytical Geometry and of The Differential and Integral Calculus , Differential Calculus, Section I, Definitions and First Principles[取自{{{2}}}]
“凡此变数中函彼变数,则此为彼之函数”(One variable is said to be a function of another variable, when the first is equal to a certain algebraic expression containing the second.)这句话,往往被讹传为出现在李善兰另一译作《代数学》中,其实并非如此,出处就是《代微积拾级》。
微分 同样是卷十,可以看到微分的定义:
函數與變數之變比例俱謂之微分 ,用彳號記之。如
[math]\displaystyle{ 戌\xlongequal{\qquad}天^三 }[/math] ,則得比例
𢓍 :
[math]\displaystyle{ :: 一 : 三天^二 }[/math] 。
𢓍 ,爲天與戌之微分。后皆仿此,用表天與戌之變比例。以一四兩率相乘,二三兩率相乘,則得
[math]\displaystyle{ \xlongequal{\qquad}三天^二 }[/math] 𢓍 。此顯函數戌之變比例,等于 三天
二 乘變數天之變比例。以
𢓍 約之,得
𢓍 / [math]\displaystyle{ \xlongequal{\qquad}三天^二 }[/math] 。此顯變數之變比例,約函數之變比例,等于函數之微係數也。如戌爲天之函數,三天 爲戌之微係數,此舉立方以㮣其餘。
[取自《代微積拾級·卷十 微分一·論函數微分·第二款》]
原文如下:
Elements of Analytical Geometry and of The Differential and Integral Calculus , Differential Calculus, Section I, Differentiation of Algebraic Functions, Proposition II - Theorem[取自{{{2}}}]
[math]\displaystyle{ \mathrm{d} }[/math] ,书中的微分号仍然是斜体[math]\displaystyle{ d }[/math] 。
书中所称“Differential Coefficient”,译作“微系数”,今天称作导数(Derivative) 。无论是中英文,这种古老的说法都已很罕见。
积分 在卷十七,定义了积分:
積分爲微分之還原,其法之要,在識別微分所由生之函數。如已得 天二 之微分爲 二天𢓍 ,則有 二天𢓍 ,即知所由生之函數爲 天二 ,而 天二 即爲積分。已得微分所由生之函數爲積分。 而積分或有常數附之,或無常數附之,既不能定,故式中恒附以常數,命爲𠰳 。𠰳 或有同數,或爲〇,須攷題乃知。𢓍 [math]\displaystyle{ \xlongequal{\qquad} 天^二 \bot }[/math] 𠰳 。來氏說今西國天算家大率不用,而惟用此禾字,取其一覽了然也。[取自《代微積拾級·卷十七 積分一·總論》]
原文如下:
Elements of Analytical Geometry and of The Differential and Integral Calculus , Integral Calculus, Section I, Integration of Monomial Differentials[取自{{{2}}}]
实际上,书中的积分号仅仅写作∫ [math]\displaystyle{ \int }[/math] 那么长。