|
|
| 第1,400行: |
第1,400行: |
|
原文如下: |
|
原文如下: |
|
{{from|A<span style{{=}}"font-size: 70%;>RTICLE</span> (157.) I<span style{{=}}"font-size: 70%;>N</span> the Differential Calculus, as in Analytical Geometry, there are two classes of quantities to be considered, viz., ''variables'' and ''constants''.<br><br>Variable quantities are generally represented by the last letters of the alphabet, ''x'', ''y'', ''z'', etc., and any values may be assigned to them which will satisfy the equations into which they enter.<br><br>Constant quantities are generally represented by the firstletters of the alphabet, ''a'', ''b'', ''c'', etc., and these always retain the same values throughout the same investigation.<br><br>Thus, in the equation of a straight line, <br><center><math>y=ax+b</math>,</center>the quantities a and b have but one value for the same line, while ''x'' and ''y'' vary in value for every point of the line.<br><br>(158.) '''One variable is said to be a ''function'' of another variable, when the first is equal to a certain algebraic expression containing the second.''' Thus, in the equation of a straight line <br><center><math>y=ax+b</math>,</center>''y'' is a function of ''x''. <br><br>So, also, in the equation of a circle, <br><center><math>y=\sqrt{R^2-x^2}</math>;</center>and in the equation of the ellipse, <br><center><math>y=\frac{B}{A}\sqrt{2Ax-x^2}</math>.</center>(159.) When we wish merely to denote that ''y'' is ''dependent'' upon ''x'' for its value, without giving the particular expression which shows the value of ''x'', we employ the notation<br><center><math>y=F(x)</math>, or <math>y=f(x)</math>,<br><span style{{=}}"text-align: left; float: left;">or</span><math>x=F(y)</math>, or <math>x=f(y)</math>,</center>which expressions are read, ''y'' is a function of ''x'', or ''x'' is a function of ''y''. |
|
{{from|A<span style{{=}}"font-size: 70%;>RTICLE</span> (157.) I<span style{{=}}"font-size: 70%;>N</span> the Differential Calculus, as in Analytical Geometry, there are two classes of quantities to be considered, viz., ''variables'' and ''constants''.<br><br>Variable quantities are generally represented by the last letters of the alphabet, ''x'', ''y'', ''z'', etc., and any values may be assigned to them which will satisfy the equations into which they enter.<br><br>Constant quantities are generally represented by the firstletters of the alphabet, ''a'', ''b'', ''c'', etc., and these always retain the same values throughout the same investigation.<br><br>Thus, in the equation of a straight line, <br><center><math>y=ax+b</math>,</center>the quantities a and b have but one value for the same line, while ''x'' and ''y'' vary in value for every point of the line.<br><br>(158.) '''One variable is said to be a ''function'' of another variable, when the first is equal to a certain algebraic expression containing the second.''' Thus, in the equation of a straight line <br><center><math>y=ax+b</math>,</center>''y'' is a function of ''x''. <br><br>So, also, in the equation of a circle, <br><center><math>y=\sqrt{R^2-x^2}</math>;</center>and in the equation of the ellipse, <br><center><math>y=\frac{B}{A}\sqrt{2Ax-x^2}</math>.</center>(159.) When we wish merely to denote that ''y'' is ''dependent'' upon ''x'' for its value, without giving the particular expression which shows the value of ''x'', we employ the notation<br><center><math>y=F(x)</math>, or <math>y=f(x)</math>,<br><span style{{=}}"text-align: left; float: left;">or</span><math>x=F(y)</math>, or <math>x=f(y)</math>,</center>which expressions are read, ''y'' is a function of ''x'', or ''x'' is a function of ''y''. |
|
|''Elements of Analytical Geometry and of The Differential and Integral Calculus'', Differential Calculus, Section I}} |
|
|''Elements of Analytical Geometry and of The Differential and Integral Calculus'', Differential Calculus, Section I, Definitions and First Principles}} |
|
|
|
|
|
<center>[[File:Elements of Analytical Geometry and of The Differential and Integral Calculus.pdf|page=124|300px]][[File:Elements of Analytical Geometry and of The Differential and Integral Calculus.pdf|page=125|300px]]</center> |
|
<center>[[File:Elements of Analytical Geometry and of The Differential and Integral Calculus.pdf|page=124|300px]][[File:Elements of Analytical Geometry and of The Differential and Integral Calculus.pdf|page=125|300px]]</center> |
| 第1,413行: |
第1,413行: |
|
同样是卷十,可以看到微分的定义: |
|
同样是卷十,可以看到微分的定义: |
|
|
|
|
|
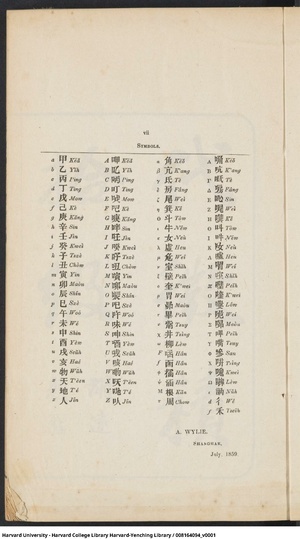
{{from|'''函數與變數之變比例俱謂之微分''',用彳號記之。如 <math>戌\xlongequal{\qquad}天^三</math>,則得比例 {{RareChar|𢓍|⿰彳天}} : [[File:Differential u.svg|16px]] <math>:: 一 : 三天^二</math>。{{RareChar|𢓍|⿰彳天}}[[File:Differential u.svg|16px]],爲天與戌之微分。后皆仿此,用表天與戌之變比例。以一四兩率相乘,二三兩率相乘,則得[[File:Differential u.svg|16px]]<math>\xlongequal{\qquad}三天^二</math>{{RareChar|𢓍|⿰彳天}}。此顯函數戌之變比例,等于 三天<sup>二</sup> 乘變數天之變比例。以{{RareChar|𢓍|⿰彳天}}約之,得{{sfrac|{{RareChar|𢓍|⿰彳天}}|[[File:Differential u.svg|16px]]}}<math>\xlongequal{\qquad}三天^二</math>。此顯變數之變比例,約函數之變比例,等于函數之微係數也。如戌爲天之函數,三天 爲戌之微係數,此舉立方以㮣其餘。|《代微積拾級·卷十 微分一·論函數微分》}} |
|
{{from|'''函數與變數之變比例俱謂之微分''',用彳號記之。如 <math>戌\xlongequal{\qquad}天^三</math>,則得比例 {{RareChar|𢓍|⿰彳天}} : [[File:Differential u.svg|16px]] <math>:: 一 : 三天^二</math>。{{RareChar|𢓍|⿰彳天}}[[File:Differential u.svg|16px]],爲天與戌之微分。后皆仿此,用表天與戌之變比例。以一四兩率相乘,二三兩率相乘,則得[[File:Differential u.svg|16px]]<math>\xlongequal{\qquad}三天^二</math>{{RareChar|𢓍|⿰彳天}}。此顯函數戌之變比例,等于 三天<sup>二</sup> 乘變數天之變比例。以{{RareChar|𢓍|⿰彳天}}約之,得{{sfrac|{{RareChar|𢓍|⿰彳天}}|[[File:Differential u.svg|16px]]}}<math>\xlongequal{\qquad}三天^二</math>。此顯變數之變比例,約函數之變比例,等于函數之微係數也。如戌爲天之函數,三天 爲戌之微係數,此舉立方以㮣其餘。|《代微積拾級·卷十 微分一·論函數微分·第二款》}} |
|
<center>[[File:Elements of Analytical Geometry and of The Differential and Integral Calculus (Chinese, 1859, 2).pdf|page=19|300px]][[File:Elements of Analytical Geometry and of The Differential and Integral Calculus (Chinese, 1859, 2).pdf|page=18|300px]]</center> |
|
<center>[[File:Elements of Analytical Geometry and of The Differential and Integral Calculus (Chinese, 1859, 2).pdf|page=19|300px]][[File:Elements of Analytical Geometry and of The Differential and Integral Calculus (Chinese, 1859, 2).pdf|page=18|300px]]</center> |
|
|-| |
|
|-| |
|
English= |
|
English= |
|
原文如下: |
|
原文如下: |
|
{{from|(170.) '''The rate of variation of a function or of any variable quantity is called its ''differential''''', and is denoted by the letter ''d'' placed before it. Thus, if<br><center><math>u=x^3</math>,</center>then<br><center><math>dx:du::1:3x^2</math>.</center>The expressions ''dx'', ''du'' are read differential of ''x'', differential of ''u'', and denote the rates of variation of ''x'' and ''u''.<br><br>If we multiply together the extremes and the means of the preceding proportion, we have<br><center><math>du=3x^2dx</math>,</center>which signifies that the rate of increase of the function ''u'' is 3''x''<sup>2</sup> times that of the variable ''x''.<br><br>If we divide each member of the last equation by ''dx'', we have<br><center><math>\frac{du}{dx}=3x^2</math>,</center>which expresses the ratio of the rate of variation of the function to that of the independent variable, and is called the ''differential coefficient'' of ''u'' regarded as a function of ''x''.|''Elements of Analytical Geometry and of The Differential and Integral Calculus'', Differential Calculus, Proposition II}} |
|
{{from|(170.) '''The rate of variation of a function or of any variable quantity is called its ''differential''''', and is denoted by the letter ''d'' placed before it. Thus, if<br><center><math>u=x^3</math>,</center>then<br><center><math>dx:du::1:3x^2</math>.</center>The expressions ''dx'', ''du'' are read differential of ''x'', differential of ''u'', and denote the rates of variation of ''x'' and ''u''.<br><br>If we multiply together the extremes and the means of the preceding proportion, we have<br><center><math>du=3x^2dx</math>,</center>which signifies that the rate of increase of the function ''u'' is 3''x''<sup>2</sup> times that of the variable ''x''.<br><br>If we divide each member of the last equation by ''dx'', we have<br><center><math>\frac{du}{dx}=3x^2</math>,</center>which expresses the ratio of the rate of variation of the function to that of the independent variable, and is called the ''differential coefficient'' of ''u'' regarded as a function of ''x''.|''Elements of Analytical Geometry and of The Differential and Integral Calculus'', Differential Calculus, Section I, Differentiation of Algebraic Functions, Proposition II - Theorem}} |
|
|
|
|
|
<center>[[File:Elements of Analytical Geometry and of The Differential and Integral Calculus.pdf|page=131|300px]]</center> |
|
<center>[[File:Elements of Analytical Geometry and of The Differential and Integral Calculus.pdf|page=131|300px]]</center> |
|
|
|
|
|
注意,时至今日,微分号为了与量区别而记作<math>\mathrm{d}</math>,书中的微分号仍然是斜体<math>d</math>。 |
|
注意,时至今日,微分号为了与量区别而记作<math>\mathrm{d}</math>,书中的微分号仍然是斜体<math>d</math>。 |
|
|
|
|
</tabber> |
|
</tabber> |
|
|
|
|
|
书中所称“Differential Coefficient”,译作“微系数”,今天称作'''导数(Derivative)'''。无论是中英文,这种古老的说法都已很罕见。 |
|
|
|
|
|
== 积分 == |
|
== 积分 == |
| 第1,436行: |
第1,439行: |
|
English= |
|
English= |
|
原文如下: |
|
原文如下: |
|
{{from|A<span style{{=}}"font-size: 70%;>RTICLE</span> (291.) T<span style{{=}}"font-size: 70%;>HE</span> Integral Calculus is the reverse of the Differential Calculus, its object being to determine the expression or function from which a given differential has been derived.<br><br>Thus we have found that the differential of ''x''<sup>2</sup> is 2''xdx'', therefore, if we have given 2''xdx'', we know that it must have been derived from ''x'', or plus a constant term.<br><br>(292.) '''The function from which the given differential has been derived, is called its ''integral''.''' Hence, as we are not certain whether the integral has a constant quantity or not added to it, we annex a constant quantity represented by C, the value of which is to be determined from the nature of the problem. <br><br>(293.) Leibnitz considered the differentials of functions as indefinitely small differences, and the sum of these indefinitely small differences he regarded as making up the function; hence the letter S was placed before the differential to show that the sum was to be taken. As it was frequently required to place S before a compound expression, it was elongated into the sign ''∫'', which, being placed before a differential, denotes that its integral is to be taken. Thus,<br><center><math>\int 2xdx = x^2+C</math>.</center>This sign ''∫'' is still retained ever by those whu reject the philosophy of Leibnitz. |''Elements of Analytical Geometry and of The Differential and Integral Calculus'', Integral Calculus, Section I}} |
|
{{from|A<span style{{=}}"font-size: 70%;>RTICLE</span> (291.) T<span style{{=}}"font-size: 70%;>HE</span> Integral Calculus is the reverse of the Differential Calculus, its object being to determine the expression or function from which a given differential has been derived.<br><br>Thus we have found that the differential of ''x''<sup>2</sup> is 2''xdx'', therefore, if we have given 2''xdx'', we know that it must have been derived from ''x'', or plus a constant term.<br><br>(292.) '''The function from which the given differential has been derived, is called its ''integral''.''' Hence, as we are not certain whether the integral has a constant quantity or not added to it, we annex a constant quantity represented by C, the value of which is to be determined from the nature of the problem. <br><br>(293.) Leibnitz considered the differentials of functions as indefinitely small differences, and the sum of these indefinitely small differences he regarded as making up the function; hence the letter S was placed before the differential to show that the sum was to be taken. As it was frequently required to place S before a compound expression, it was elongated into the sign ''∫'', which, being placed before a differential, denotes that its integral is to be taken. Thus,<br><center><math>\int 2xdx = x^2+C</math>.</center>This sign ''∫'' is still retained ever by those whu reject the philosophy of Leibnitz. |''Elements of Analytical Geometry and of The Differential and Integral Calculus'', Integral Calculus, Section I, Integration of Monomial Differentials}} |
|
|
|
|
|
实际上,书中的积分号仅仅写作<span style="font-family:serif;">''∫''</span>,没有写得像今天的<math>\int</math>那么长。 |
|
实际上,书中的积分号仅仅写作<span style="font-family:serif;">''∫''</span>,没有写得像今天的<math>\int</math>那么长。 |